En esta opción podemos modelar en dos dimensiones como se forma la elipse a partir de un hipercicloide
viernes, 7 de junio de 2013
Hipercicloide
En esta opción podemos modelar en dos dimensiones como se forma la elipse a partir de un hipercicloide
CÁLCULOS GEODESICOS
jueves, 11 de abril de 2013
Esferoides tumorales para evaluar la terapia del cáncer
Esferoides tumorales para evaluar la terapia del cáncer
por el doctor Gabriel L. Fiszman
El cáncer de mama es la primera causa de muerte por patología oncológica en la mujer y representa un 20,8% de todos los tumores malignos.
Las características biológicas de la célula tumoral se investigan, fundamentalmente, utilizando el crecimiento de líneas celulares estables en monocapa (2 dimensiones). A pesar que este modelo in vitro ha permitido obtener mucha información valiosa respecto a mecanismos relacionados con el crecimiento maligno, no representa real y completamente el crecimiento de un tumor in vivo. Los tumores sólidos crecen en un orden espacial tridimensional (3D) con contactos célula-célula muy íntimos, una organización compleja de la matriz extracelular y una distribución irregular de oxígeno y nutrientes. Considerando estas diferencias, nos dedicamos a generar condiciones particulares de cultivo in vitro que permiten el crecimiento en 3D de células tumorales (esferoides). Este modelo tiene la particularidad de reflejar la situación fisiopatológica in vivo de microrregiones tumorales y de sitios metastásicos avasculares.
Las características biológicas de la célula tumoral se investigan, fundamentalmente, utilizando el crecimiento de líneas celulares estables en monocapa (2 dimensiones). A pesar que este modelo in vitro ha permitido obtener mucha información valiosa respecto a mecanismos relacionados con el crecimiento maligno, no representa real y completamente el crecimiento de un tumor in vivo. Los tumores sólidos crecen en un orden espacial tridimensional (3D) con contactos célula-célula muy íntimos, una organización compleja de la matriz extracelular y una distribución irregular de oxígeno y nutrientes. Considerando estas diferencias, nos dedicamos a generar condiciones particulares de cultivo in vitro que permiten el crecimiento en 3D de células tumorales (esferoides). Este modelo tiene la particularidad de reflejar la situación fisiopatológica in vivo de microrregiones tumorales y de sitios metastásicos avasculares.
Nuestro grupo de trabajo utiliza esferoides tumorales (ET) a partir de líneas célulares de adenocarcinomas mamarios murinos y humanos con el objetivo de evaluar mecanismos de acción y de resistencia a drogas y otros tratamientos oncológicos. Comprobamos que el origen histológico de la línea celular es una característica fundamental que condiciona su potencial crecimiento en 3D así como su morfología, por ej. grado de compactación del esferoide. Analizando la cinética de crecimiento de ET de diferentes líneas celulares, con técnicas de inmunofluorescencia e inmunohistoquímica, observamos que los esferoides crecen con una morfología geométrica en una organización concéntrica de células proliferantes (en crecimiento continuo), quiescentes (detenidas en su crecimiento) y muertas (por necrosis, apoptosis y otros mecanismos de muerte celular programada) hacia el centro del esferoide, el cual presenta condiciones de baja presión de oxígeno o hipoxia. La hipoxia es una característica frecuente de los tumores humanos, generalmente asociada con un pronóstico desfavorable, probablemente debido a una penetración insuficiente o nula de drogas.
Nuestro grupo de trabajo, utilizando esferoides de células tumorales de mama humano que expresan el receptor HER2, estudia el efecto del núcleo hipóxico sobre la respuesta al tratamiento con el anticuerpo monoclonal Trastuzumab (anti-HER2). Los resultados obtenidos nos están permitiendo entender factores y mecanismos que participan en la resistencia de las células hipóxicas al tratamiento.
Durante la progresión neoplásica, células del sistema inmune como los monocitos/macrófagos, son atraídas hacia el entorno tumoral donde inician una respuesta contra las células neoplásicas. Sin embargo, frecuentemente las células tumorales evaden la maquinaria inmune citotóxica. Los macrófagos asociados al tumor (TAM) tienen la capacidad de eliminar las células tumorales en los inicios del crecimiento del tumor, luego durante la progresión, modifican su actividad favoreciendo el crecimiento tumoral.
Los esferoides mixtos (células tumorales cocultivadas con diferentes poblaciones celulares del microambiente tumoral) ofrecen un modelo útil y suplementario al uso de animales para mimetizar diferentes aspectos del crecimiento de tumores humanos in vivo.
En este sentido, utilizando los ET, estudiamos los diferentes factores asociados al tumor que modulan la diferenciación y activación de monocitos/macrófagos, algunos de ellos inducidos bajo condiciones específicas de estrés celular como la hipoxia. Con ese objetivo, cuando infiltramos los ET con monocitos de dadores normales, observamos que los TAM indujeron una disminución en el crecimiento de los esferoides en etapas tempranas, mayor al 50%, comparado con los ET controles sin infiltrar.
En este sentido, utilizando los ET, estudiamos los diferentes factores asociados al tumor que modulan la diferenciación y activación de monocitos/macrófagos, algunos de ellos inducidos bajo condiciones específicas de estrés celular como la hipoxia. Con ese objetivo, cuando infiltramos los ET con monocitos de dadores normales, observamos que los TAM indujeron una disminución en el crecimiento de los esferoides en etapas tempranas, mayor al 50%, comparado con los ET controles sin infiltrar.
Nuestro trabajo parte de la hipótesis que el crecimiento celular en una arquitectura 3D que contiene un núcleo hipóxico, permitirá evidenciar una regulación diferencial entre la población de células tumorales y las células inmunes infiltrantes, generándose cambios tanto fenotípicos como proteómicos en ambas poblaciones. Estos cambios estarían asociados a las diferentes etapas del crecimiento tumoral así como a otras variables, como la histología del tumor, la evolución/tamaño del esferoide, aparición de focos hipóxicos/necróticos, condicionando en su conjunto la respuesta al tratamiento.
TOPOGRAFIA EN BASE DEL DATUM WGS 1984
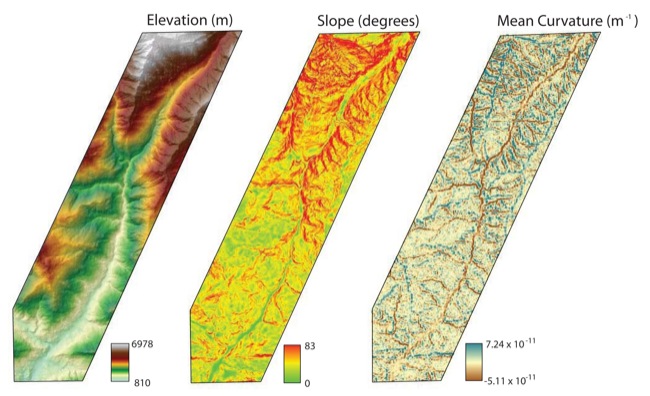
Ver Imagen original en tamaño completo
Figura 3. Modelo de elevación digital (DEM), la pendiente y la curvatura de las redes para el valle de Modi Khola (Resolución: 25 m). Sistema de coordenadas geográficas: WGS 1984 UTM Zona 44N. Proyección: Transversa de Mercator.
DATUM GEODESICO
Bueno, hablamos sobre la superficie curva de la Tierra, por lo que ahora vamos a añadir (superficie de la tierra) a nuestro sistema de coordenadas 3D.
La forma de la tierra es bastante complicado. El estudio de su forma, tamaño y campo de gravedad es todo un campo de estudio ( Geodesia ) y está cubierto en otro módulo, pero, para resumir, a partir de diversos estudios, sabemos que la mejor manera de representar la forma de la Tierra matemáticamente es mediante el uso de un elipsoide.
Un elipsoide es simplemente una elipse gira alrededor de su eje menor (b).
Si ubicamos el centro de nuestra elipsoide para coincidir con el centro de nuestro sistema de coordenadas cartesianas 3D (también el centro de la masa de la Tierra) hemos definido lo que se conoce como un "datum geodésico.
(Fuente - Trimble Navigation Ltd.)
El uso de un "punto de referencia geodésico ', cualquier punto de la superficie de la Tierra tiene un x, y, z valor de coordenadas, y que el valor de coordenadas se puede traducir en un Latitud (φ), Longitud (λ) y una altura (h) anterior, en o incluso por debajo de la superficie del modelo matemático.
(Fuente - Trimble Navigation Ltd.)
Datums geodésicos se utilizan para el posicionamiento horizontal. La componente vertical se refiere tradicionalmente al nivel medio del mar. elevaciones se discuten en detalle en el geoide módulo.
FUNCIONAMIENTO DE UN SIG
FUNCIONAMIENTO DE UN SIG
El SIG funciona como una base de datos con información geográfica (datos alfanuméricos) que se encuentra asociada por un identificador común a los objetos gráficos de un mapa digital. De esta forma, señalando un objeto se conocen sus atributos e, inversamente, preguntando por un registro de la base de datos se puede saber su localización en la cartografía.
La razón fundamental para utilizar un SIG es la gestión de información espacial. El sistema permite separar la información en diferentes capas temáticas y las almacena independientemente, permitiendo trabajar con ellas de manera rápida y sencilla, y facilitando al profesional la posibilidad de relacionar la información existente a través de la topología de los objetos, con el fin de generar otra nueva que no podríamos obtener de otra forma.
Las principales cuestiones que puede resolver un Sistema de Información Geográfica, ordenadas de menor a mayor complejidad, son:
- Localización: preguntar por las características de un lugar concreto.
- Condición: el cumplimiento o no de unas condiciones impuestas al sistema.
- Tendencia: comparación entre situaciones temporales o espaciales distintas de alguna característica.
- Rutas: cálculo de rutas óptimas entre dos o más puntos.
- Pautas: detección de pautas espaciales.
- Modelos: generación de modelos a partir de fenómenos o actuaciones simuladas.
Por ser tan versátiles, el campo de aplicación de los Sistemas de Información Geográfica es muy amplio, pudiendo utilizarse en la mayoría de las actividades con un componente espacial. La profunda revolución que han provocado las nuevas tecnologías ha incidido de manera decisiva en su evolución.
SIG
¿Qué es un SIG?
Un Sistema de Información Geográfica (SIG o GIS, en su acrónimo inglés [Geographic Information System]) es una integración organizada de hardware, software ydatos geográficos diseñada para capturar, almacenar, manipular, analizar y desplegar en todas sus formas la información geográficamente referenciada con el fin de resolver problemas complejos de planificación y de gestión
Análisis de Datos
Análisis de datos de direcciones
Con las direcciones geocodificadas, puede visualizar las ubicaciones de las direcciones espacialmente y comenzar a reconocer patrones dentro de la información. Para ello, sólo debe ver la información o utilizar algunas de las herramientas de análisis disponibles en ArcGIS. También puede visualizar la información de la dirección basándose en ciertos parámetros, lo que le permite analizar la información aun más.
 |
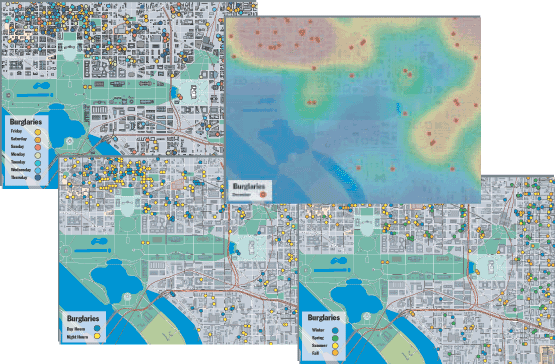El registro anual de crímenes se creó, en principio, con la geocodificación de una tabla de base de datos de robos que contenía una dirección para cada uno. Las capturas de pantalla anteriores muestran cómo se presentaban las direcciones geocodificadas en base a la hora, la temporada o el día de la semana para asistir la planificación de la prevención del crimen. Se pueden utilizar herramientas de análisis adicionales de ArcGIS para analizar la información más profundamente y así identificar los patrones. Los datos base de esta aplicación de muestra pertenecen a Tele Atlas y Vexcel Corp.
¿Qué es la geocodificación?
La geocodificación es el proceso de transformar una descripción de una ubicación (por ejemplo, un par de coordenadas, una dirección o un nombre de un lugar) en una ubicación de la superficie de la Tierra. Se puede geocodificar introduciendo una descripción de una ubicación a la vez o proporcionando muchas de ellas al mismo tiempo en una tabla. Las ubicaciones que se obtienen se transforman en entidades geográficas con atributos, que se pueden utilizar para la representación cartográfica o el para análisis espacial.
Con la geocodificación, puede buscar varios tipos de ubicaciones de manera rápida. Los tipos de ubicaciones que puede buscar incluyen: puntos de interés o nombres de un diccionario geográfico, como montañas, puentes y negocios; coordenadas basadas en latitud y longitud o en otros sistemas de referencia, por ejemplo, el Sistema de referencia de cuadrícula militar (MGRS) o el Sistema de cuadrícula nacional de los EE.UU.; y direcciones, que pueden presentarse en varios estilos y formatos, por ejemplo, intersecciones de calles, números de casas junto con números de calles y códigos postales.
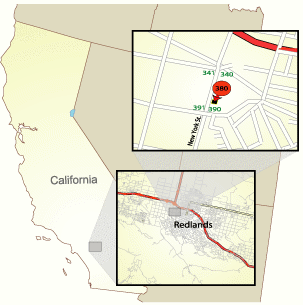
Datums Locales
Datums locales
Un datum local alinea su esferoide para que se ajuste estrechamente a la superficie de la tierra en un área determinada. Un punto de la superficie del esferoide se asocia a una posición determinada en la superficie de la tierra. Este punto se conoce como punto del origen del datum. Las coordenadas del punto del origen son fijas y todos los demás puntos se calculan a partir de él.
 |
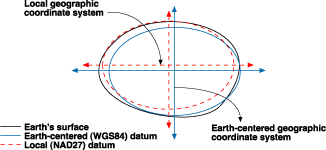El origen del sistema de coordenadas de un datum local no se encuentra en el centro de la tierra. El centro del esferoide de un datum local está desplazado respecto al centro de la tierra. NAD 1927 y el Datum Europeo de 1950 (ED 1950) son datums locales. NAD 1927 se diseñó para que se ajustara a América del Norte razonablemente bien, mientras que ED 1950 se creó para su uso en Europa. Dado que un datum local alinea tan estrechamente su esferoide a una área determinada de la superficie de la tierra, no es adecuado para su uso fuera del área para la que se diseñó.
Datum
Aunque un esferoide ofrece una aproximación a la forma de la tierra, un datum define la posición del esferoide relativa al centro de la tierra. Un datum proporciona un marco de referencia para medir las ubicaciones en la superficie de la tierra. Define el origen y la orientación de las líneas de latitud y longitud.
Siempre que cambie el datum o, más correctamente, el sistema de coordenadas geográficas, los valores de coordenadas de los datos cambiarán. Las siguientes son las coordenadas en grados/minutos/segundos (DMS) de un punto de control en Redlands, California, en el Datum de Norteamérica de 1983 (NAD 1983 o NAD83):
A continuación, el mismo punto en el Datum de Norteamérica de 1927 (NAD 1927 o NAD27):
El valor de longitud difiere en aproximadamente 3 segundos, mientras que el valor de latitud difiere en aproximadamente 0,05 segundos.
NAD 1983 y el Sistema Geodésico Mundial de 1984 (WGS 1984) son idénticos para la mayoría de las aplicaciones. Las siguientes son las coordenadas para el mismo punto de control sobre la base de WGS 1984:
Datums geocéntricos
En los últimos 15 años, los datos de los satélites han proporcionado nuevas mediciones para definir el esferoide que mejor se ajusta a la tierra, que relaciona las coordenadas con el centro de masa de la tierra. Un datum centrado en la tierra o geocéntrico utiliza el centro de masa de la tierra como origen. El último datum desarrollado, ampliamente utilizado, es WGS 1984. Sirve como marco para la medición mundial de ubicaciones.
Creación de Mapas precisos Atraves de Esferoides
La Tierra ha sido estudiada en numerosas ocasiones con el objetivo de conocer mejor las características de su superficie y sus irregularidades. Dichos estudios han resultado en el cálculo de diversos esferoides que representan el planeta. Por lo general, se elige uno u otro esferoide dependiendo del país o área que se desee representar. Un esferoide apropiado para la representación de una región determinada puede no ser apropiado para la representación de otras regiones. Hasta no hace mucho, los datums utilizados en América del Norte se basaban en el esferoide calculado por Clarke en 1866. El semieje mayor del esferoide Clarke 1866 tiene 6.378.206,4 metros y el semieje menor 6.356.583,8 metros.
Debido al efecto gravitatorio y a las variaciones en las características de su superficie, la Tierra no es una esfera perfecta y tampoco un esferoide perfecto. Los satélites nos han permitido descubrir diversas desviaciones elípticas en la Tierra. Por ejemplo, el Polo Sur está más cerca del Ecuador que el Polo Norte. Los esferoides calculados por satélite están reemplazando los esferoides medidos tradicionalmente a ras de suelo. Por ejemplo, el nuevo esferoide estándar para América del Norte es el Sistema Geodésico de Referencia (GRS por sus siglas en inglés) de 1980 (GRS 1980), cuyos radios son de 6.378.137,0 y 6.356.752,31414 metros. La International Union for Geodesy and Geophysics (Unión Internacional de Geodesia y Geofísica) estableció en 1979 los parámetros del GRS 1980.
Al cambiar el esferoide de un sistema de coordenadas, se modificarán todos los valores de coordenadas de sus entidades. Por ello, muchas organizaciones no han cambiado aún a los esferoides más recientes, que son no obstante más precisos.
Esferas y Esferoides
La superficie de un sistema de coordenadas geográficas se define a partir de una esfera o un esferoide. Aunque un esferoide representa la Tierra con mayor precisión, ésta es tratada a veces como una esfera para simplificar los cálculos matemáticos. Es plausible considerar la Tierra como una esfera para la creación de mapas a pequeña escala (inferior a 1:5.000.000). A dichas escalas, la diferencia existente entre una esfera y un esferoide no plantea problemas detectables en el mapa. Sin embargo, para mantener la precisión en mapas de mayor escala (1:1.000.000 o más), es necesario representar la Tierra como un esferoide. Si nos mantenemos entre ambas escalas, la decisión de utilizar una esfera o un esferoide dependerá de la finalidad del mapa y la precisión deseada en los datos.
Definición de esferoide
La esfera se forma a partir de una circunferencia, mientras que el esferoide (o elipsoide) se forma a partir de una elipse.
 |
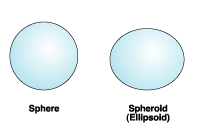Un esferoide o elipsoide es una esfera achatada por los polos.
|
La forma de una elipse queda definida por dos radios. El radio más largo se denomina semieje mayor y el más corto se denomina semieje menor.
 |
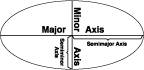El semieje mayor o radio ecuatorial es la mitad del eje mayor. El semieje menor o radio polar es la mitad del eje menor.
|
Cuando la elipse rota alrededor de su semieje menor aparece un esferoide. Los esferoides también reciben el nombre de elipsoides oblatos de revolución. El siguiente gráfico muestra los semiejes mayor y menor de un esferoide.
 |
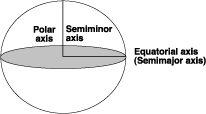El semieje mayor se sitúa sobre el plano ecuatorial y el semieje menor es perpendicular al mismo.
|
Un esferoide queda definido por su semieje mayor (a) y su semieje menor (b), o por (a) y su aplanamiento. El aplanamiento es equivalente a la diferencia de longitud entre los dos ejes, expresada como fracción o decimal. El aplanamiento (f) se obtiene de la siguiente manera:
El aplanamiento es un valor pequeño, de manera que suele utilizarse el valor 1/f en su lugar. Estos son los parámetros de esferoide establecidos por el Sistema Geodésico Mundial (WGS por sus siglas en inglés) de 1984 (WGS 1984 o WGS84):
El valor del aplanamiento puede estar comprendido entre 0 y 1. Un valor de aplanamiento de 0 supone que los dos ejes son iguales, lo cual resultaría en una esfera. El valor de aplanamiento de la Tierra es de aproximadamente 0,003353. Otra cantidad que, como el aplanamiento, describe la forma de un esferoide es el cuadrado de la excentricidad (e)2. Queda representado de la siguiente forma:
 |
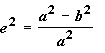Datums Mas Utilizados
Cuando se inventaron las primeras proyecciones cartográficas, se asumió incorrectamente que la Tierra era plana. Posteriormente, se revisó esta hipótesis y se llegó a la conclusión de que la Tierra era una esfera perfecta. En el siglo XVIII, se descubrió que no era totalmente redonda. Así es como nació el concepto del esferoide cartográfico.
Para representar las ubicaciones de la superficie de la Tierra con mayor precisión, los cartógrafos estudiaron la forma de la Tierra (geodesia) y crearon el concepto del esferoide. Un datum vincula un esferoide a una parte determinada de la superficie de la Tierra. Los datums más recientes se han diseñados para ajustarse también a la superficie de toda la Tierra.
Los datum utilizados normalmente en Norteamérica son:
- Datum de Norteamérica (NAD) de 1927, que utiliza el esferoide Clarke 1866
- NAD 1983, que utiliza el esferoide del Sistema Geodésico de Referencia (GRS) de 1980
- Sistema Geodésico Mundial (WGS) 1984, que utiliza el esferoide del WGS 1984
En la actualidad, los esferoides se desarrollan a partir de mediciones de satélites y son más precisos que los diseñados en los siglos XIX y XX.
Los términos "sistema de coordenadas geográficas" y "datum" suelen utilizarse indistintamente.
Las coordenadas de una ubicación cambian en función del datum y el esferoide en que se basen, incluso si se utilizan la misma proyección cartográfica y los mismos parámetros de proyección. Por ejemplo, las siguientes coordenadas geográficas son para la ciudad de Bellingham, Washington utilizando tres datums diferentes:
Datum
|
Latitud
|
Longitud
|
|---|---|---|
NAD 1927
|
48.7440490722656
|
-122.466903686523
|
NAD 1983
|
48.7438798543649
|
-122.46818353793
|
WGS 1984
|
48.7438798534299
|
-122.46818353793
|
Coordenadas Proyectadas
Un sistema de coordenadas proyectadas se define sobre una superficie plana de dos dimensiones. A diferencia de un sistema de coordenadas geográficas, un sistema de coordenadas proyectadas posee longitudes, ángulos y áreas constantes en las dos dimensiones. Un sistema de coordenadas proyectadas siempre está basado en un sistema de coordenadas geográficas basado en una esfera o un esferoide.
En un sistema de coordenadas proyectadas, las ubicaciones se identifican mediante las coordenadas x, y en una cuadrícula, con el origen en el centro de la cuadrícula. Cada posición tiene dos valores de referencia respecto a esa ubicación central. Uno especifica su posición horizontal y el otro su posición vertical.
Proyecciones Cartograficas
Los sistemas de coordenadas, también denominados proyecciones cartográficas, son designaciones arbitrarias para datos espaciales. Su finalidad es la de proporcionar una base común de comunicación sobre un lugar determinado o área de la superficie de la Tierra. El aspecto más importante al trabajar con sistemas de coordenadas consiste en saber cuál es la proyección y en tener la información correcta del sistema de coordenadas asociado a un dataset. Existen dos tipos de sistemas de coordenadas: geográficos y proyectados.
En un sistema de coordenadas geográficas se utiliza una superficie esférica tridimensional para definir ubicaciones en la Tierra. Un sistema de coordenadas geográficas incluye una unidad angular de medida, un meridiano base y un datum (basado en un esferoide). Los valores de latitud y longitud hacen referencia a un punto en un sistema de coordenadas geográficas. La longitud y la latitud son ángulos medidos desde el centro de la Tierra hasta un punto de la superficie de la Tierra. Los ángulos se suelen medir en grados (o en grados centesimales).
Datum y Esferoide
El datum y el esferoide subyacentes que se utilizan como referencia para un dataset pueden cambiar los valores de las coordenadas. A continuación se muestra un ejemplo en el que se utiliza la ciudad de Bellingham, Washington. Compare las coordenadas en grados decimales para Bellingham utilizando NAD27, NAD83 y WGS84. Es evidente que, mientras NAD83 y WGS84 expresan coordenadas casi idénticas, NAD27 es bastante diferente, porque los datums y esferoides utilizados expresan de manera diferente la forma subyacente de la Tierra.
Datum
|
Longitud
|
Latitud
|
|---|---|---|
NAD 1927
|
-122,46690368652
|
48,7440490722656
|
NAD 1983
|
-122,46818353793
|
48,7438798543649
|
WGS 1984
|
-122,46818353793
|
48,7438798534299
|
La longitud es la medición del ángulo desde el meridiano base en Greenwich, Inglaterra, hasta el centro de la Tierra y, a continuación, hacia el oeste hasta la longitud de Bellingham, Washington. La latitud es la medición del ángulo formado desde el ecuador hasta el centro de la Tierra y, a continuación, hacia el norte hasta la latitud de Bellingham, Washington.
Si la superficie de la Tierra en Bellingham está abultada hacia afuera, las mediciones angulares en grados decimales desde Greenwich y el ecuador serán algo mayores. Si la superficie en Bellingham está deprimida, los ángulos serán algo menores. Se trata de dos ejemplos de cómo cambian las coordenadas en función del datum.
Smiejes de la Tierra Geoide
El geoide se define como la superficie del campo de gravedad de la Tierra, que es aproximadamente igual que el nivel medio del mar. Es perpendicular a la dirección de la atracción gravitatoria. Dado que la masa de la Tierra no es uniforme en todos los puntos y la dirección de gravedad cambia, la forma del geoide es irregular.
Haga clic en el vínculo siguiente para acceder a un sitio web mantenido por la NOAA, National Oceanographic & Atmospheric Administration (Administración Nacional Oceánica y Atmosférica). Este sitio web tiene vínculos a imágenes que muestran interpretaciones del geoide bajo América del Norte. el http://www.ngs.noaa.gov/GEOID/GEOID96/geo-indx.html
Para simplificar el modelo se han ideado diversos esferoides o elipsoides. Estos términos se utilizan de forma intercambiable. En el resto de este artículo, se utilizará el término “esferoide”.
Un esferoide es una forma de tres dimensiones creada a partir de una elipse de dos dimensiones. La elipse es un óvalo, con un eje mayor (el eje más largo) y un eje menor (el eje más corto). Si se hace girar la elipse, la forma de la figura girada es el esferoide.
El semieje mayor es la mitad de la longitud del eje mayor. El semieje menor es la mitad de la longitud del eje menor.
En el caso de la Tierra, el semieje mayor es el radio desde el centro de la Tierra hasta el ecuador, mientras que el semieje menor es el radio desde el centro de la Tierra hasta el polo.
Un esferoide determinado se distingue de otro por las longitudes de los semiejes mayores y menores. Por ejemplo, compare el esferoide Clarke 1866 con los esferoides GRS 1980 y WGS 1984, sobre la base de las siguientes mediciones (en metros).
Esferoide
|
SemiejeM
|
Semieje m
|
|---|---|---|
Clarke 1866
|
6378206,4
|
6356583,8
|
GRS80 1980
|
6378137
|
6356752,31414
|
WGS84 1984
|
6378137
|
6356752,31424518
|
miércoles, 6 de marzo de 2013
martes, 26 de febrero de 2013
lunes, 25 de febrero de 2013
jueves, 21 de febrero de 2013
INTERFAZ GRÁFICA DEL PROYECTO
INTERFAZ GRÁFICA DEL ELIPSOIDE
INTERFAZ GRÁFICA DEL ESFEROIDE
INTERFAZ GRÁFICA DEL ESFEROIDE EN 3D
MODELO DEL GEOIDE EN 3D - LUEGO DE ESTABLECER SUS PUNTOS DE SU ANOMLIA GRAVITATORIA
PERSPECTIVA DEL GEOIDE EN LA PARTE SUPERIOR
miércoles, 20 de febrero de 2013
LISTADO DE REQUERIMIENTOS
LISTADO DE REQUERIMIENTOS PARA EL FUNCIONAMIENTO DEL SOFTWARE
- Clave del programa
- Distancia focal
- Distancia del eje mayor del Elipsoide
- Distancia del eje menor del Elipsoide
- F o (Achatamiento Polar)
- Valor de a (Distancia del origen al foco, desde la linea ecuatorial)
- Valor de b (Distancia del origen a la parte superior de la elipse)
- Puntos de Coordenadas Esférica
- Volumen del Esferoide
- Fuerza de Gravedad
- Anomalía gravitatoria
- Inclinación del Eje del Geoidal
- Ubicación Geocartesiana
martes, 19 de febrero de 2013
PROYECTO
OBJETIVO QUE SE REQUIERE
Diseñar un programa que pueda modelar y generar geoides en tres dimensiones
Desarrollando un software en java, que principalmente diseñe o cree un elipsoide, y con base en este generar un esferoide de tal manera que al aplicar las anomalías gravitacionales sobre este modelo en determinadas coordenadas podamos generar el geoide.
Para determinar el volumen del Geoide, el estudio de coordenadas geodésicas, el calculo de ciertas áreas y las diferentes interpretaciones morfológicas a través del tiempo.
COMO GENERAR GEOIDES Y ESFEROIDES
GEOIDE
La forma del geoide puede determinarse por medio de:
- Medidas de las anomalías gravitatorias midiendo la magnitud de la intensidad de la gravedad en numerosos puntos de la superficie terrestre. Dado que es similar a un esferoide (esfera achatada por los polos) la aceleración de la gravedad va aumentando desde el ecuador hasta los polos. Estas mediciones de la gravedad terrestre tienen que ser corregidas para eliminar las anomalías locales debido a variaciones de la densidad.
- Mediciones astronómicas: Se fundan en medir la vertical del lugar y ver sus variaciones. Esta variación se relaciona con su forma.
- Medición de las deformaciones producidas en la órbita de los satélites causadas porque la Tierra no es homogénea. Así se ha determinado un geoide con decenas de abultamientos o depresiones respecto al esferoide teórico. Estas irregularidades son menores de 100 metros.
ESFEROIDE
Es importante recordar que las superficies de revolución son aquellas que se generan haciendo girar una curva alrededor de un eje. Algunos geofísicos consideran al esferoide como modelo geométrico de la tierra y no solo a este sino también a la esfera, por ello el esferoide tiene meridiana principal y ecuador. Elipse: curva cerrada en forma oval.
Achatamiento
Es la magnitud adimensional:
Siendo el aplanamiento la inversa del achatamiento.
Así, el diámetro ecuatorial es 43 km mayor que el diámetro polar. Es por ello que los puntos más alejados del centro de la Tierra y, por ende, los puntos que tienen menor gravedad) vienen siendo el volcán Chimborazo y otros puntos elevados del continente americano en la zona ecuatorial (y en menor grado, el Kilimandjaro y otras montañas en África).
Latitud y latitud geocéntrica
Al ser la Tierra aproximadamente un esferoide, la latitud o ángulo que forma un lugar con el ecuador terrestre y la latitud geocéntrica o ángulo que forma el lugar con el ecuador visto desde el centro de la Tierra no es el mismo.
Para relacionarlos se introduce la variable auxiliar u:
Si H es la altura sobre el nivel del mar en metros del observador y 
la distancia al centro de la Tierra, se cumple:
la distancia al centro de la Tierra, se cumple:
ANOMALÍA GRAVITATORIA
Se define como anomalía gravitatoria a la diferencia entre el valor de gravedad observado (gobs) en un determinado lugar de un planeta —generalmente un punto en su superficie— y la gravedad teórica (γ), obtenida de un modelo que contempla las dimensiones, masa y rotación del planeta: 
. Una anomalía positiva de gravedad indica la presencia de un cuerpo con exceso de masa respecto a la masa del modelo de referencia. Mediante el modelado numérico del campo gravitatorio es posible determinar la estructura interna de los planetas.
. Una anomalía positiva de gravedad indica la presencia de un cuerpo con exceso de masa respecto a la masa del modelo de referencia. Mediante el modelado numérico del campo gravitatorio es posible determinar la estructura interna de los planetas.
La anomalía gravitatoria es medida a través de medidas in situ o bien mediante satélite. Suele presentarse en forma de mapas y es expresada habitualmente en unidades de miligal (1mGal = 10-5 m/s2). Además se le suelen aplicar ciertas correcciones como la de Airy y Bouguer que facilitan la interpretación de los datos.
Anomalía gravitatoria observada
La medida, generalmente sobre la superficie de la Tierra, en relación a un valor de referencia.
Anomalía de aire libre
Corresponde a la diferencia entre el valor de gravedad observado y el valor de gravedad teórico corregido por la altura del valor medido de g respecto a una superficie de referencia (que puede ser el geoide) mediante la aplicación de una corrección del gradiente de gravedad normal (corrección de aire libre). La aproximación de primer orden se expresa como: 
Donde 0,3086 es el gradiente de gravedad normal expresado en mGal/m y h es la cota del punto donde se realizó la observación de la gravedad en metros.
Anomalía de Bouguer
Esta anomalía no sólo tiene en cuenta la variación de la gravedad con la altura, como la de aire libre, sino que también tiene en cuenta las masas presentes entre el punto de observación y la superficie de referencia (geoide). Al aplicar esta corrección, la anomalía restante es representativa sobre todo de cambios de densidad a nivel cortical y de cambios en el grosor de la corteza terrestre. La anomalía de Bouguer es generalmente negativa en orógenos compresivos como los Pirineos o los Andes debido a que la topografía de éstos está isostáticamente compensada por una raíz cortical entre 4 y 8 veces más gruesa. Igual que un iceberg necesita ser más profundo cuanto más hielo sobresale sobre el nivel del mar, el engrosamiento de la corteza compensa la topografía terrestre (isostasia). Este engrosamiento implica un déficit de masa en la base de la corteza, pues ésta es menos densa que el manto terrestre).
Anomalía isostática
Como la de Bouguer, pero sustrayendo además la atracción gravitatoria que produciría un engrosamiento teórico de la corteza terrestre que compense isostáticamente la topografía. La anomalía resultante suele interpretarse como fruto de cambios de densidad a niveles por debajo de la corteza.
GEOGRAFÍA Y GRAVIMETRIA DEL GEOIDE
En geografía y disciplinas afines o derivadas (geodesia, cartografía, topografía, etc.) actualmente un geoide es la superficie física definida mediante el potencial gravitatorio, de modo que sobre él hay en todos los puntos la misma atracción terrestre. Se excluyen los fenómenos orogénicos, por lo que las montañas no se incluyen en el mismo. Gráficamente se puede definir como la superficie de los mares en calma prolongada bajo los continentes. Geométricamente es casi una esferoide de revolución (esfera achatada por los polos) con irregularidades menores de 100 metros.
Técnicamente y utilizando herramientas gravimétricas se denomina geoide a la superficie física definida por un determinado potencial gravitatorio (constante en toda la superficie). Para definir el geoide, se adopta arbitrariamente el valor de potencial cuyo geoide asociado se aproxima más a la superficie de los océanos (la superficie media del mar, prescindiendo del oleaje, las mareas, las corrientes y la rotación terrestre, coincide casi exactamente con una superficie equipotencial). La forma del geoide no coincide necesariamente con la topografía terrestre, modelada por fuerzas endógenas (tectónica de placas) y exógenas (agentes geomorfológicos). Geométricamente, el geoide es parecido a un esferoide (esfera achatada por los polos).
QUE ES EL GEOIDE?
¿Qué es el Geoide?
Es la figura geométrica de tres dimensiones que modela la forma y tamaño de la Tierra lo más exacto
posible. Pero resulta que esta figura terrestre es algo que cambia constantemente por causas como el
movimiento de placas tectónicas y hasta efectos climatológicos, por lo cual se hace necesario definir ahora
lo que entendemos por forma de la Tierra. Si el agua del mar pudiera permanecer totalmente estática por un momento alrededor del planeta y tuviera condiciones ideales como temperatura constante,concentración de sales homogénea y sin perturbaciones por efectos atmosféricos, entonces su superficie
materializaría una superficie denivel del campo gravitacional (o superficie equipotencial) a lo que llamamos forma de la Tierra. El geoide es, precisamente, esa El geoide para el área mexicana y sus aplicaciones superficie que cubre por completo el globo, incluso por debajo de la topografía continental, y en cualquiera de sus puntos esperpendicular a la línea de plomada o dirección de la gravedad.http://www.inegi.org.mx/inegi/contenidos/espanol/prensa/contenidos/articulos/geografica/geoide03.pdf
Se denomina geoide (etimológicamente, del griego : γεια —tierra— ειδος —forma, apariencia— ‘forma que tiene la tierra’) al cuerpo de forma casi esferica aunque con un ligero achatamiento en los polos (esferoide), definido por la superficie equipotencial del campo gravitatorio terrestre que coincide con el nivel medio del mar. Por lo antedicho se suele considerar que geoide es la forma teórica, determinada geodesicamente del planeta Tierra.
Suscribirse a:
Entradas (Atom)